二叉树

为什么使用二叉树

• 有序数组中插入数据过慢
• 在链表中查找太慢

用树解决什么问题

既能像链表那样快速的插入和删除，又能像有序数组那样快速查找， 树实现了这些特点，成为最有意思的数据结构之一。

树是什么

树是范畴更广的图的特例，不过这里先不考虑图。

组成部分：

• 根：树顶端的节点称为”根”
• 路径：顺着连接节点的边从一个节点走到另一个节点，所经过的节点顺序排列就称为”路径”
• 父节点：顾名思义，对于二叉树，一个节点有且只有一个父节点
• 子节点：顾名思义，对于二叉树，一个父节点最多可以有两个子节点
• 叶结点：没有子节点的节点称为”叶子节点”或者简称”叶结点”
• 子树：每个子节点都可以作为子树的根，它和它所有的子节点、以及子节点的子节点统称为”子树”
• 访问：当程序控制流程到达某个节点时，就称为”访问”这个节点
• 遍历：遵循某种特定的顺序访问树中所有节点
• 层：一个节点的层数是指从根开始到这个节点有多少”代”
• 关键字：对象中通常有一个数据域被称为关键字值

常用操作

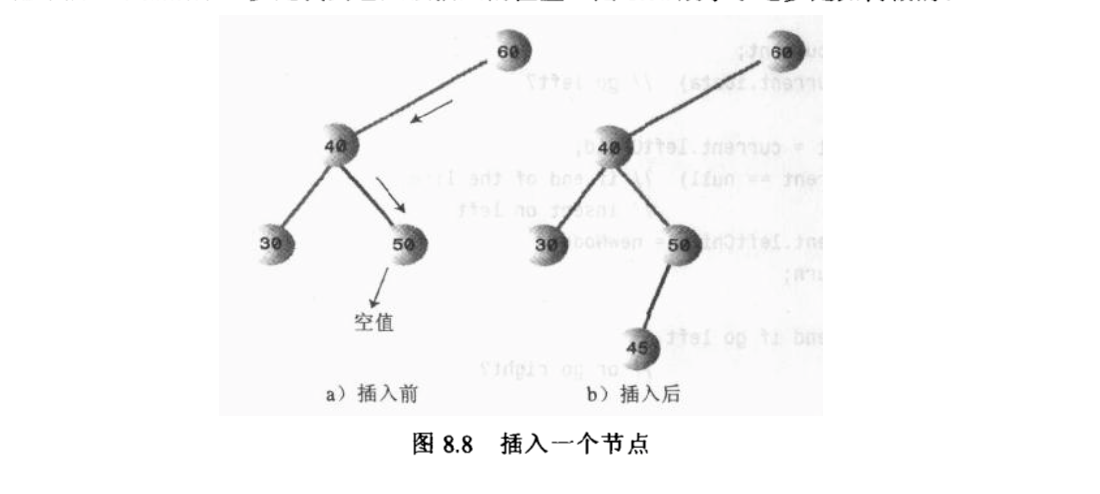
插入节点

插入节点的时候，循环遍历判断是应该找左节点还是右节点就行

  public void insert(int id, double dd) {
    Node newNode = new Node();
    newNode.iData = id;
    newNode.fData = dd;
    if (root == null) {
      root = newNode;
    } else {
      Node current = root;
      Node parent;
      while (true) {
        parent = current;
        if (id < current.iData) {
          current = current.leftChild;
          if (current == null) {
            parent.leftChild = newNode;
            return;
          }
        } else {
          current = current.rightChild;
          if (current == null) {
            parent.rightChild = newNode;
            return;
          }
        }
      }
    }
  }

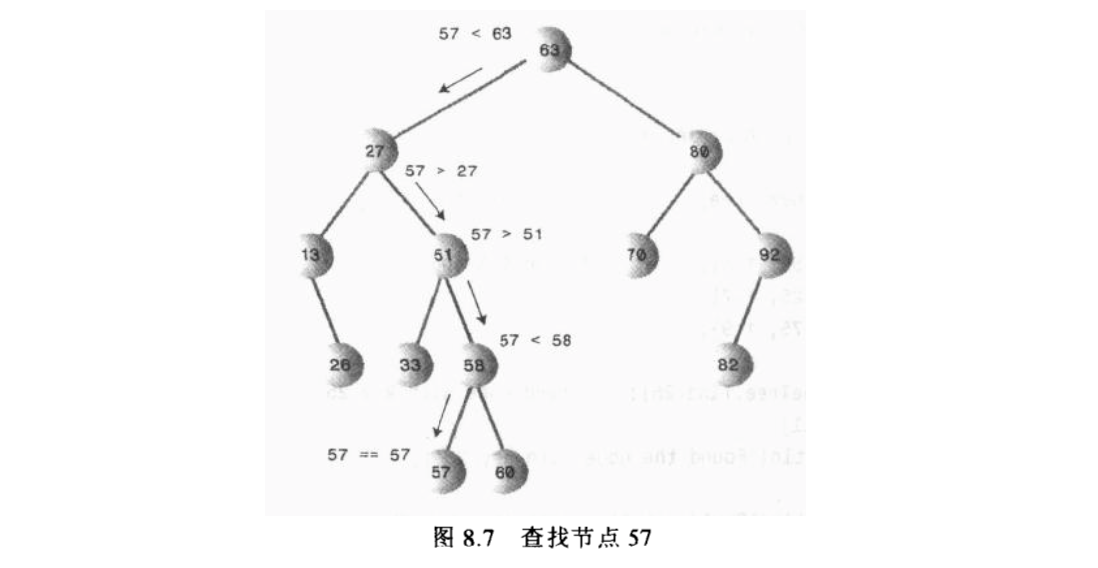
查找节点

比较当前节点值，小的话找左边，大的话找右边

  public Node find(int key) {
    Node current = root;
    while (current.iData != key) {
      if (key < current.iData) {
        current = current.leftChild;
      } else {
        current = current.rightChild;
      }
      // ？这个和直接返回 current 有什么区别？
      if (current == null) {
        return null;
      }
      return current;
    }
    return null;
  }

遍历树

遍历树是按照一种特定顺序访问树的每一个节点，并不常用，但在某些情况下是有用的，而且比较有理论意义。

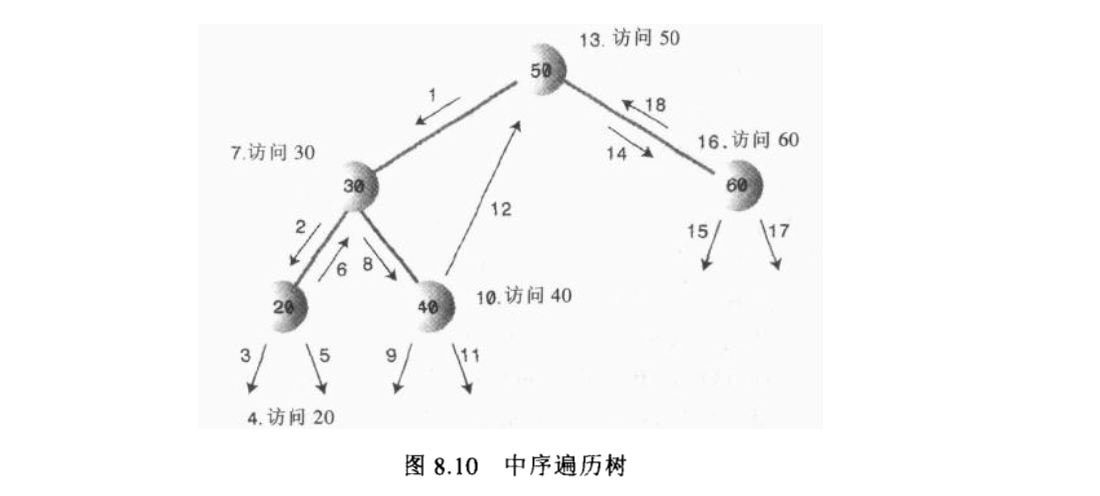
中序遍历

中序遍历二叉搜索树会使所有节点按关键字升序被访问到，如果希望在二叉树中创建有序的数据序列， 这是一种方法。遍历树的最简单方法是递归的方法，用递归的方法遍历整棵树要用一个节点作为参数。 初始化时这个节点是根。遍历可以用于任何二叉树，而不只是二叉搜索树。这个遍历的原理不关心节点的 关键字的值，只看这个节点是否有子节点。这个方法只需要做三件事：

• 调用自身来遍历节点的左子树
• 访问这个节点
• 调用自身来遍历节点的右子树

  /**
   * 中序遍历：A*(B+C)
   */
  private void inOrder(Node localRoot){
    if (localRoot!=null){
      inOrder(localRoot.leftChild);
      System.out.println(localRoot);
      inOrder(localRoot.rightChild);
    }
  }

前序遍历

  /**
   * 前序遍历：*A+BC
   */
  private void preOrder(Node localRoot){
    if (localRoot!=null){
      System.out.println(localRoot);
      inOrder(localRoot.leftChild);
      inOrder(localRoot.rightChild);
    }
  }

后序遍历

  /**
   * 后序遍历：ABC+*
   */
  private void postOrder(Node localRoot){
    if (localRoot!=null){
      inOrder(localRoot.leftChild);
      inOrder(localRoot.rightChild);
      System.out.println(localRoot);
    }
  }

算术表达式

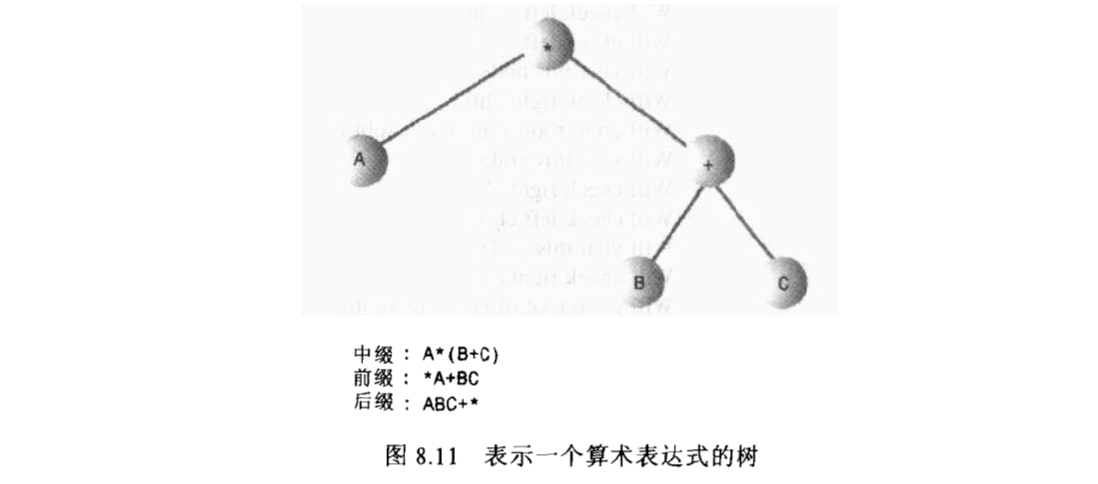
• 中序遍历：A*(B+C)
• 前序遍历：*A+BC
• 后序遍历：ABC+*

删除节点

删除节点是二叉搜索树常用的一般操作中最复杂的，但是，删除节点在很多树的应用中又非常重要， 所以要详细研究并总结特点。删除节点有三种情况需要考虑：

• 该节点是叶结点（没有子节点）
• 该节点有一个子节点
• 该节点有两个子节点

没有子节点

没有子节点的时候，只需要直接删除就行，也就是将父节点的这个子节点的连接置为空。 唯一需要考虑的就是检查一下是不是根节点。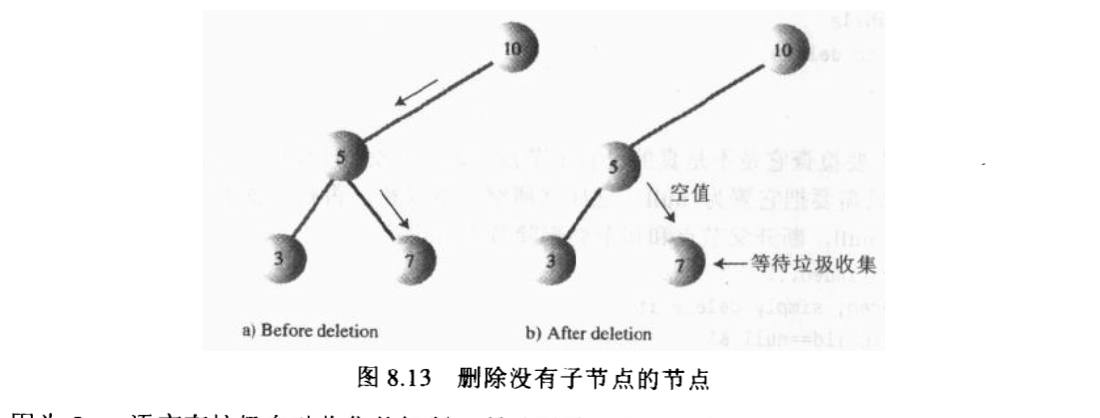

一个子节点

如果是一个子节点，因为子节点左边的肯定也在父节点左边，子节点右边的肯定也在父节点右边， 所以只需要将被删除节点的父节点连接到被删除节点的子节点就行，也需要检查一下是否是根节点。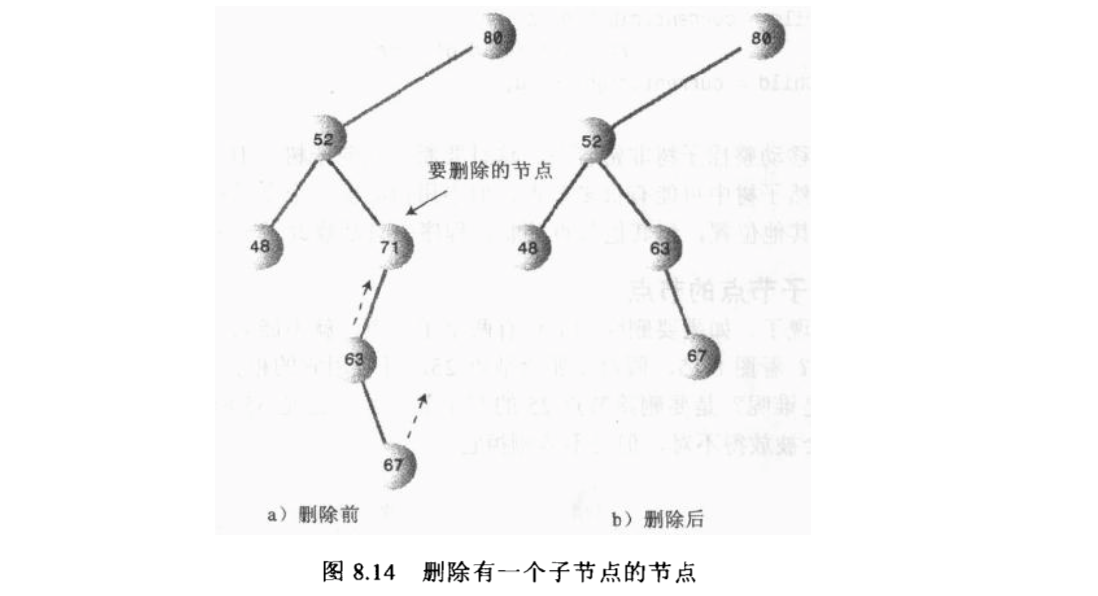

两个子节点

两个子节点的时候，情况就比较复杂。 先要找到被删除节点后的子节点中最小的那个节点，作为后继节点，也就是用这个节点顶替被删除节点的位置。 为什么是所有节点中最小的节点作为后继节点？因为符合最小的这个值才符合二叉树插入值后的结果： 被删除节点的父节点的值小于后继节点的值，且后继节点的值小于其他所有节点的值，这样其他的所有节点 都可以作为这个后继节点的右子节点。那么谁是后继节点的左子节点呢？那就是被删除节点原来的左子节点。

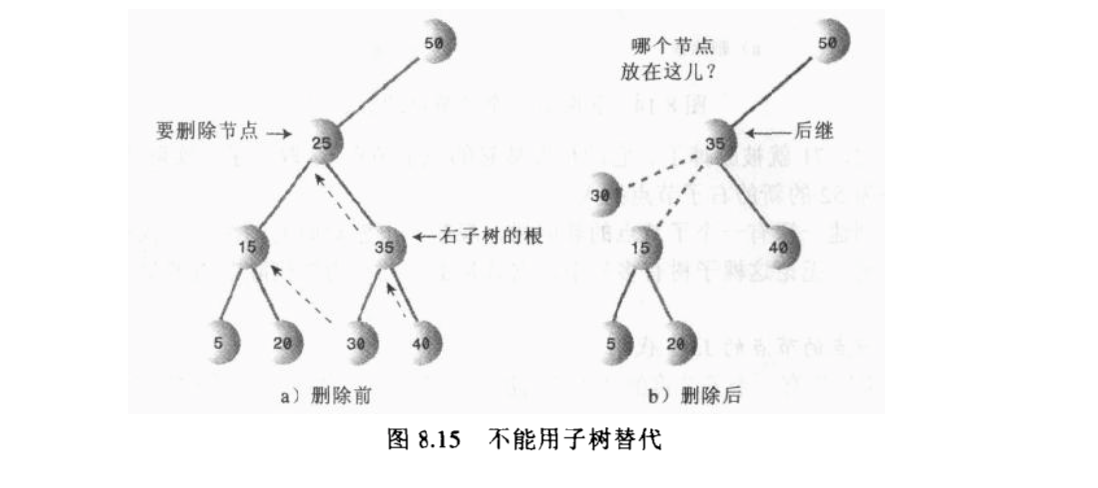
查找后继节点的方法，以及将后继节点移动到被删除节点的位置的示意，但这种情况是后积节点没有子节点的情况， 所以直接将后积节点移动过去就行：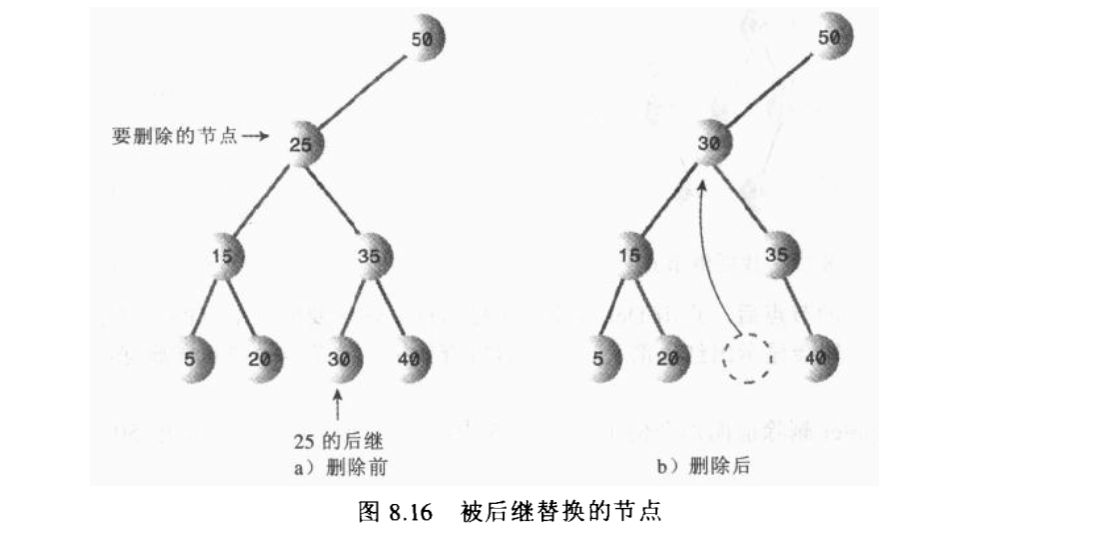

那么如果后继节点有子节点的情况呢？比如，有一个右子节点，那么需要将这个右子节点作为后继节点的父节点 的左子节点，然后后继节点放在被删除节点的位置上。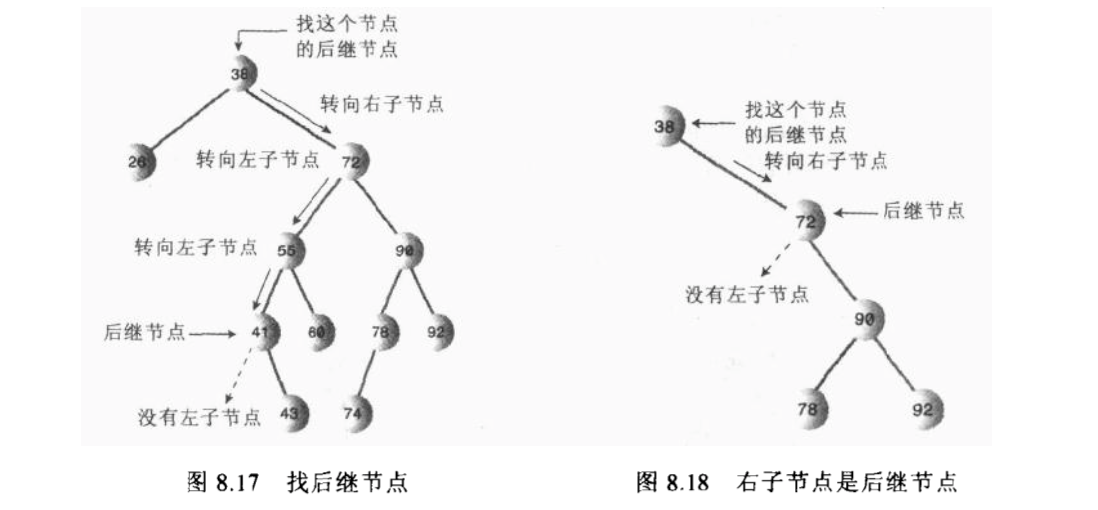

这里有一个需要注意的就是，将寻找后积节点的功能抽离成一个单独的方法，在这个方法中，做了两部分工作， 第一寻找到这个后继节点，第二如果后继节点不是被删除节点的右子节点，那么需要建立关联： 后继节点的右子节点挂在父节点的左子节点上，被删除节点的右子节点挂在后积节点的右子节点上。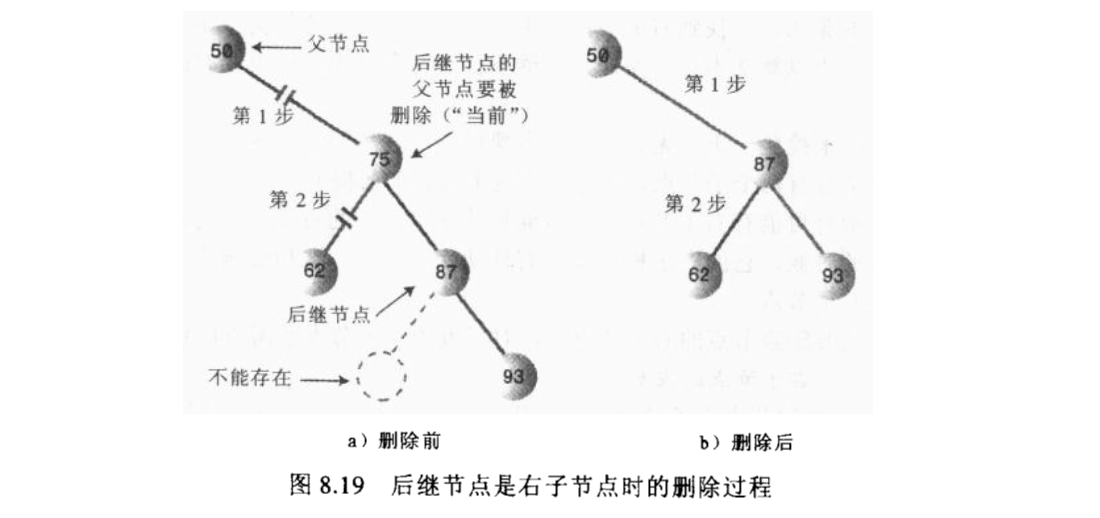

具体代码查看源码：Tree.java

删除是必要的吗

因为删除是相当棘手的操作，因为太过复杂，可以再node类中增加一个Boolean的字段，如isDeleted， 要删除一个节点的时候，就把此节点的这个字段置为true。那么在查找的时候先判断这个节点是不是已经被 删除了，这样，删除的节点不会改变树的结构。这种方法获取有些逃避责任，但如果树中没有那么多删除操作 时，这也不失为一个好方法。

用数组表示树

用数组的方法树，节点存在数组中，而不是由引用相连。节点在数组中的位置对应于它在树中的位置。 下标为0的节点是根，下标为1的节点是根的左子节点，以此类推，按照从左到右的顺序存储树的每一层：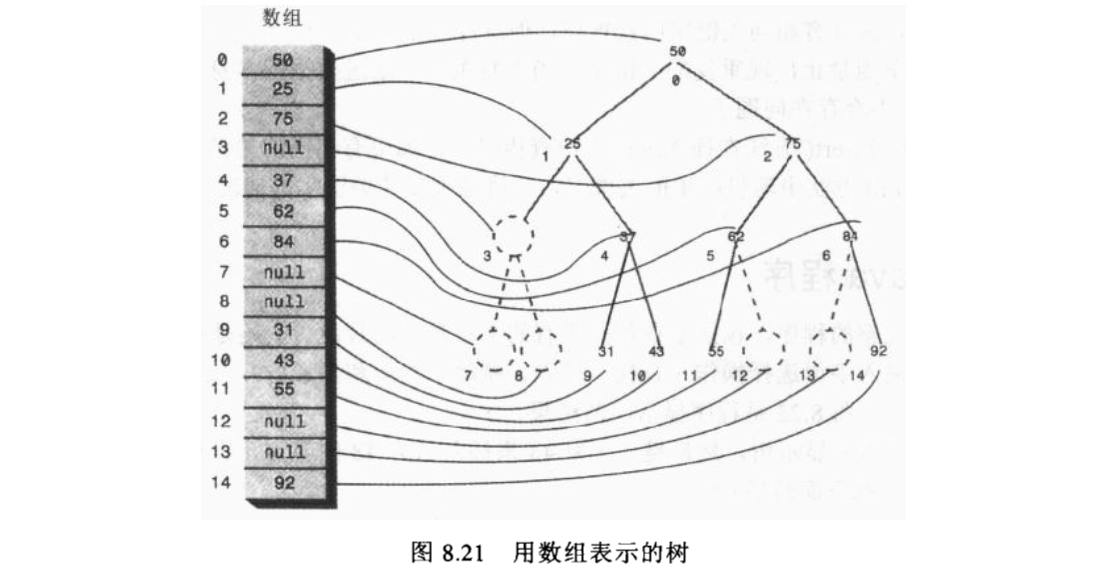

基于这种思想，找节点的子节点和父节点可以利用简单的算术计算他们在数组中的索引值。设节点索引值为index，则：

• 节点的左子节点是：2*index+1
• 节点的右子节点是：2*index+2
• 节点的父节点是： (index-1)/2

缺点是浪费存储空间，而且如果有删除操作，那么将会移动特别多的元素。

参考资料

• Java数据结构和算法