二叉树中，每个节点有一个数据项，最多有两个子节点。如果允许每个节点可以有跟多的数据项和更多的 子节点，就是多叉树(multiway tree)。2-3-4 树就是多叉树，他每个节点最多有四个子节点和三个 数据项。

首先，它像红黑树一样是平衡树，它的效率比红黑树稍差，但编程容易。其次，更重要的是，通过学习2-3-4 树可以更容易地理解B树。

2-3-4 树的介绍

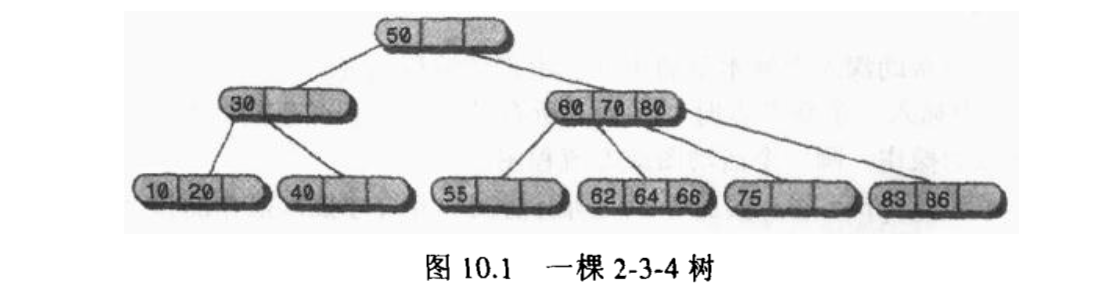
图中上面的三个节点有子节点，底层的六个节点都是叶结点，没有子节点。2-3-4树中所有的叶结点 总是在同一层上。

名字的含义

2-3-4树名字中的2、3和4是指一个节点可能含有的子节点的个数。对非叶结点有三种可能的情况：

• 有一个数据项的节点总是有两个子节点
• 有两个数据项的节点总是有三个子节点
• 有三个数据项的节点总是有四个子节点

简而言之，非叶结点的子节点数总是比它含有的数据项多1。或者，用符号表示这个规则，设子节点链接的 个数是 L ，数据项的个数是 D ，那么 L = D+1。比较来说，叶结点没有子节点，然而它可能 含有一个、两个或三个数据项，空节点是不会存在的。因为2-3-4树最多可以有四个子节点的节点，也可以 称它为 4叉树。

2-3-4 树的组织

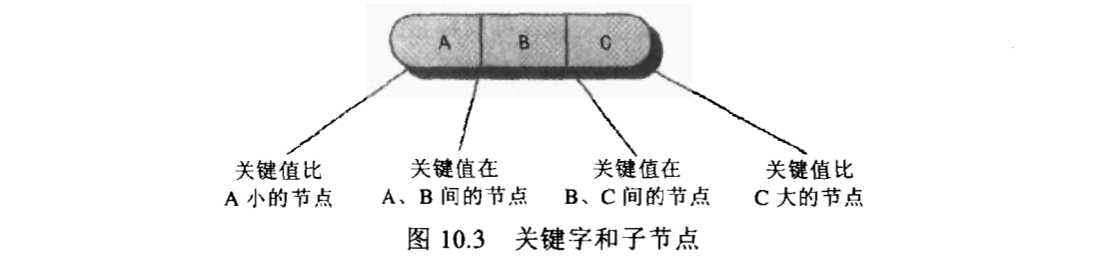
树结构中很中啊哟的一点就是它的链与自己数据项的关键字值之间的关系：

• 原二叉树的规则
  • 关键字值比某个节点值小的都在这个节点左子节点为根的子树上
  • 关键字值比某个节点值大的都在这个节点右子节点为根的子树上
• 2-3-4 增加的规则
  • 根是 child0 的子树的所有子节点的关键字值小于key0
  • 根是 child1 的子树的所有子节点的关键字值大于key0并且小于key1
  • 根是 child2 的子树的所有子节点的关键字值大于key1并且小于key2
  • 根是 child3 的子树的所有子节点的关键字值大于key2

2-3-4 树的操作

搜索

查找特定关键字值的数据项和在二叉树中的搜索过程相似。

插入

插入的时候可能需要移动其他数据项

节点分裂

如果往下寻找要插入位置的路途中，节点已经满了，插入就变得复杂了，法伤这种情况时，节点必须分裂。

2-3-4 树 和 红黑树

他们两个看起来可能完全不同，但是某种意义上，他们又是完全相同的。一个可以通过应用一些简单的规则 变成另一个，而且使他们保持平衡的操作也是一样的。数学上称他们为同构。在历史上，2-3-4树先被 提出；后来红黑树由它发展而来。

2-3-4 树转变为 红黑树

通过三条规则进行转换：

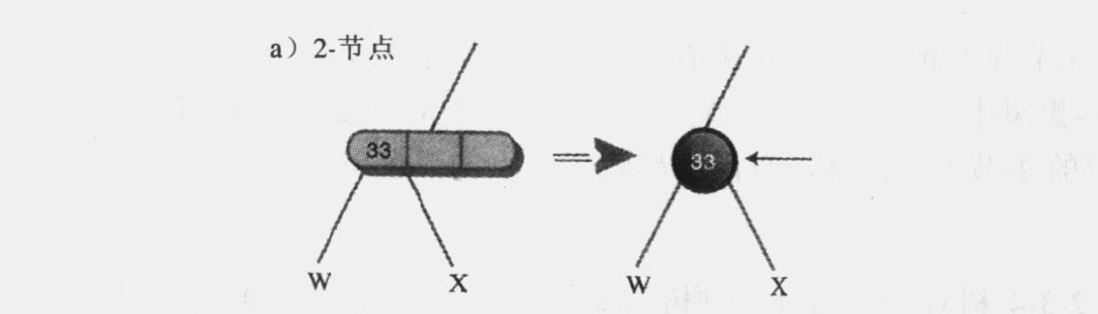
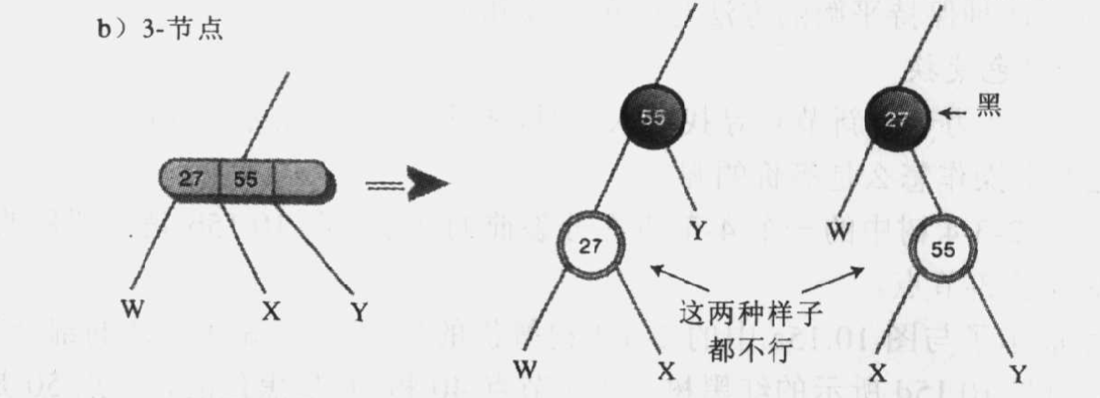
• 把2-3-4树中的每个2-节点转化成红黑树的黑色节点。图 10.13 a
• 把每个3-节点转化成一个子节点和一个父节点。子节点有两个自己的子节点，父节点有另外一个子节点。 那个节点变成子节点或父节点都无所谓，子节点涂成红色，父节点涂成黑色。
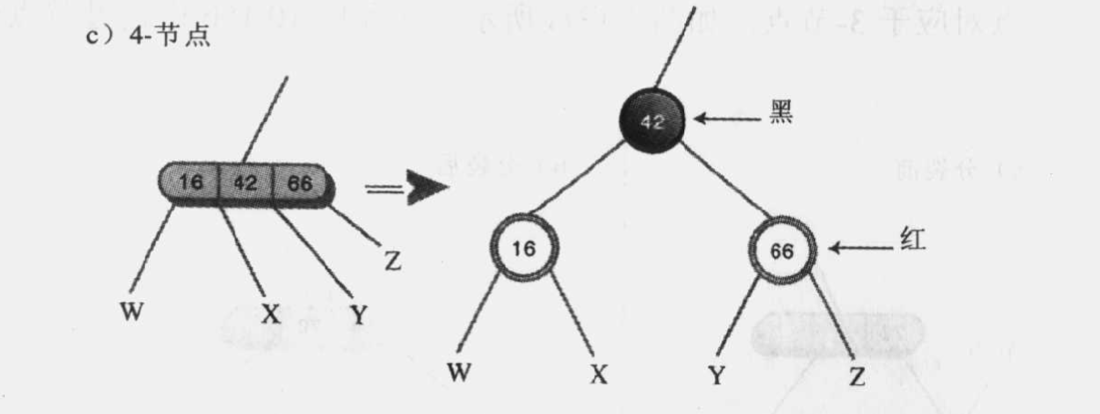
• 把每个4-节点转化成一个父节点和两个子节点。每个子节点都有两个自己的子节点。和前面一样，子节点 涂成红色，父节点涂成黑色。

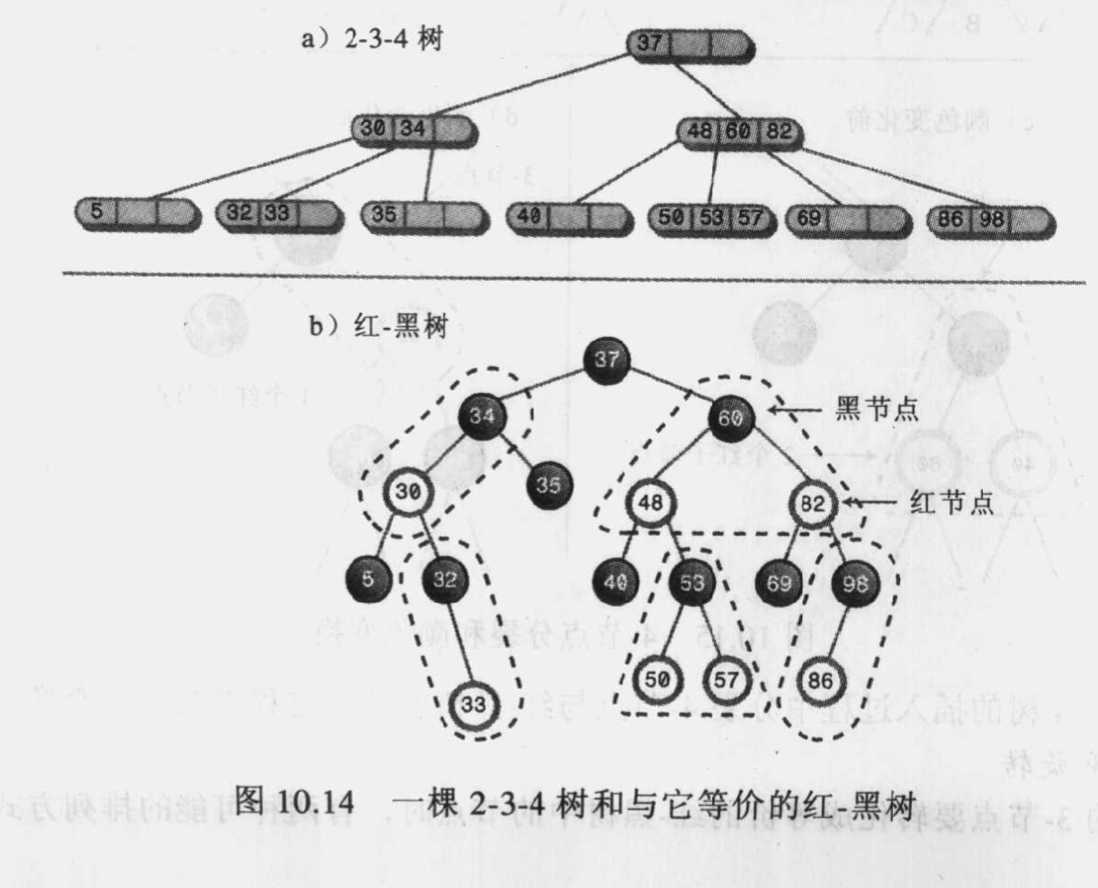
操作的等价性

不仅红黑树的结构与2-3-4树对应，而且两种树的操作也是一样的。2-3-4树用节点分裂保持平衡，红黑树 中两种保持平衡的方法是颜色交换和旋转。

4-节点分裂和颜色变换：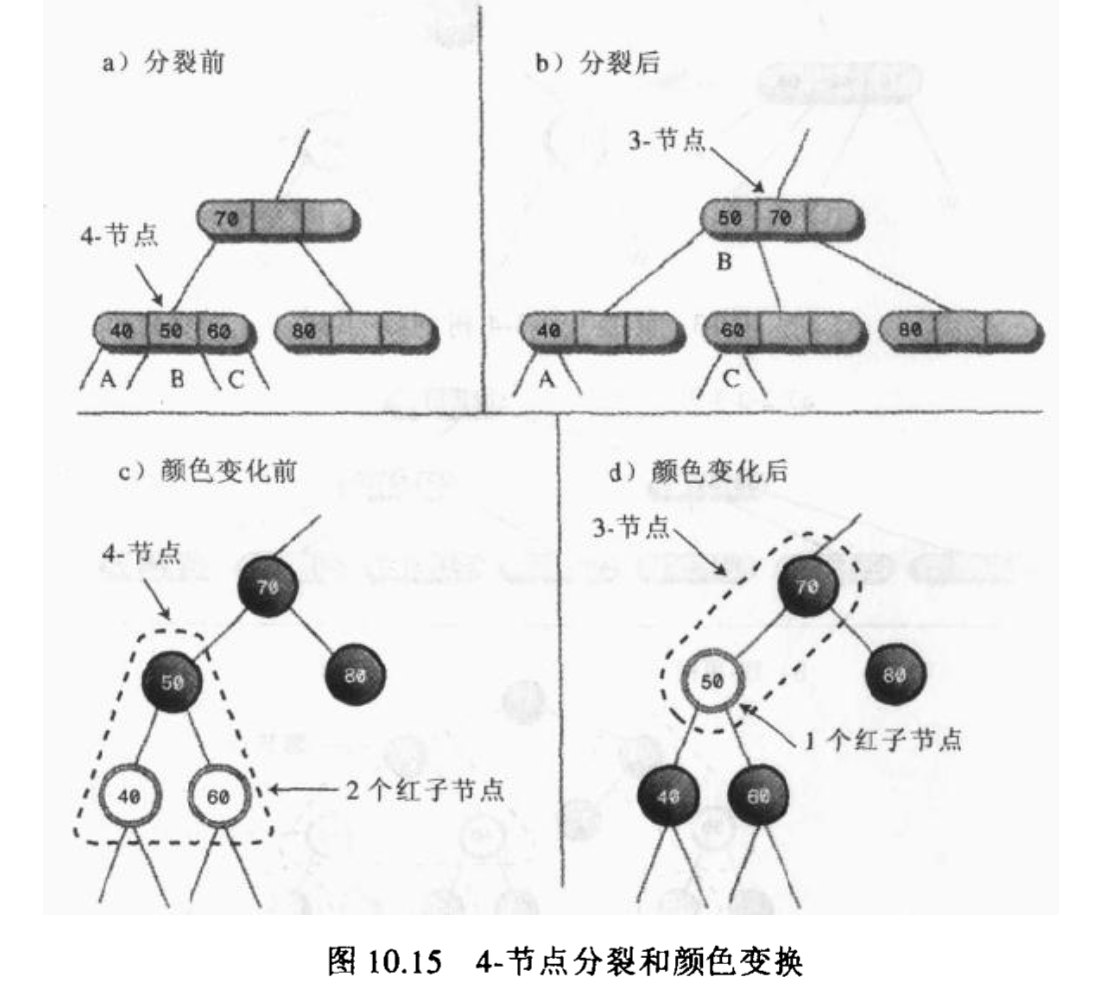

3-节点分裂和颜色变换：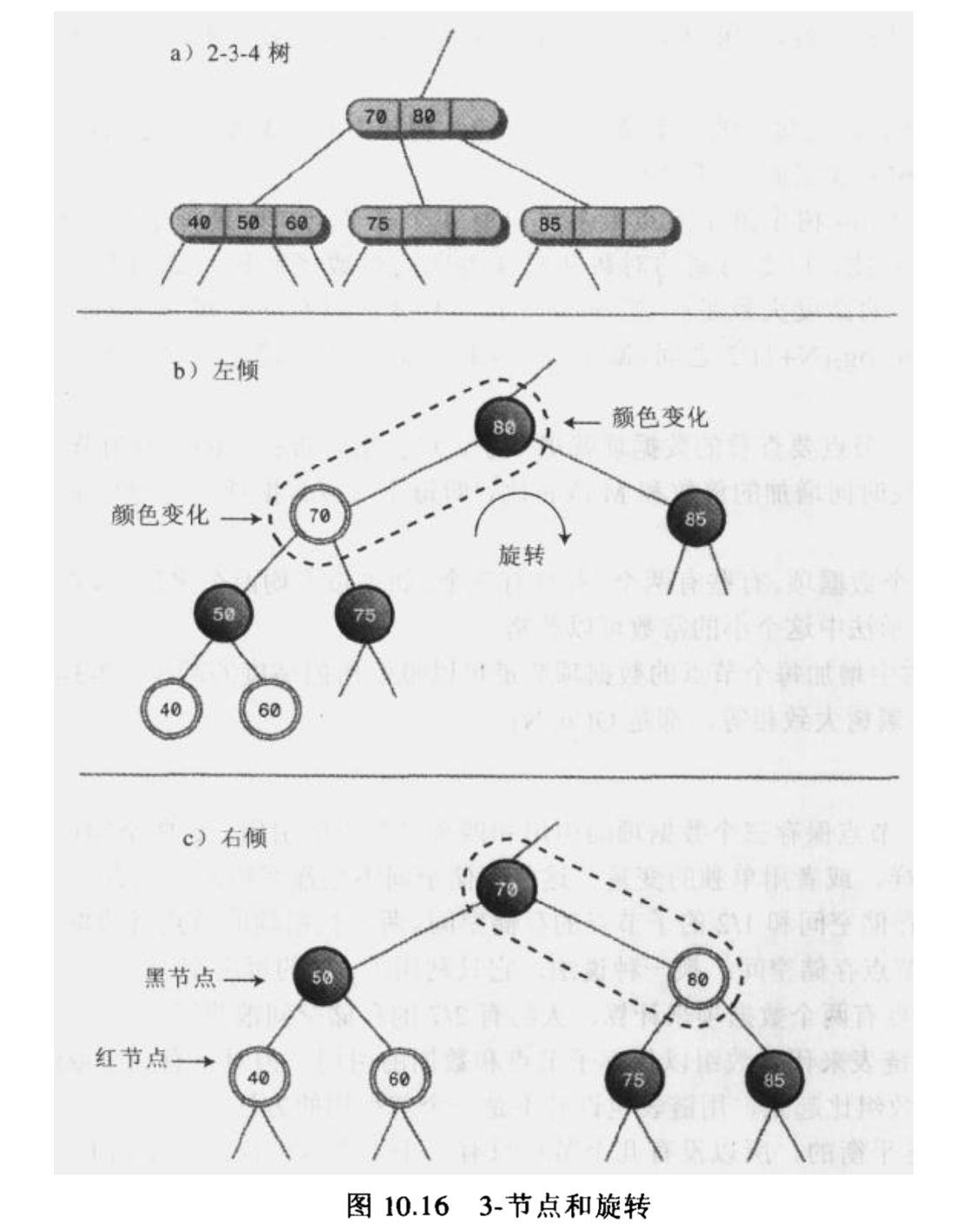

2-3-4树的效率

参考资料

• Java数据结构和算法 - 2-3-4 树
• Java数据结构和算法